개요
오랜만에 돌아온 origin series 입니다.
이번 글의 주제는 ‘압축 알고리즘’인데요, 갑자기 압축이라는 주제에 꽂히게 된 이유는 ‘압축 알고리즘의 르네상스’라는 글을 너무 재밌게 봐서 압축 알고리즘은 어떻게 변해왔는지 궁금증이 생겼기 때문입니다.
사실 컴퓨터 과학을 공부하기 이전에도 사진 파일들을 압축하면서 ‘그냥 데이터 덩어리일 뿐인데 어떤 방식으로 용량이 작아지는 거지?‘라는 의문을 가진 적이 있었는데 드디어 이 의문에 대해 마주하게 되었네요.
글의 독자는 다음과 같습니다.
- 초기 압축의 기초가 되는 알고리즘이 궁금해요.
- 압축 알고리즘이 왜 중요해지고 있는지 알고 싶어요.
손실 압축(lossy compression)과 무손실 압축(lossless compression)
먼저 데이터 압축의 사전적 의미는 무엇일까요? 위키에 따르면 다음과 같습니다.
데이터를 더 적은 저장 공간에 효율적으로 기록하기 위한 기술, 또는 그 기술의 실제 적용을 가리킨다.
이 압축은 ‘데이터의 손실 유무’에 따라서 손실 압축과 무손실 압축으로 나뉘는데요:
먼저 손실 압축은 특정 정보, 특히 중복 정보를 영구적으로 제거하여 파일의 용량을 줄이는 방법입니다.
사람은 지구 상의 모든 색상을 포토샵처럼 상세하게 색을 구별하거나(마비노기 유저들은 가능할 것 같지만), 절대 음감이라고 해서 모든 주파수를 들을 수 없습니다.
그 부분을 이용해 음악이나 영상과 같은 매체에서 구별하기 어려운 색차나 주파수를 손실시켜서 용량을 줄이는 압축 방식입니다.
이러한 특성때문에 압축을 반복하게 되면 손실이 누적되어 원본과는 큰 차이가 발생하게 되죠.
반면 무손실 압축은 명칭 그대로 손실이 없는 압축 방식입니다. 원본 그대로를 저장하지 않는데 용량을 어떤 식으로 줄이는 걸까요?
뒤에 다른 알고리즘을 소개하겠지만 ‘런 렝스 부호화(Run-length encoding, RLE)‘를 예시로 무손실 압축의 원리를 알아보겠습니다.
런 렝스 부호화는 데이터에서 같은 값이 연속해서 나타나는 것을 그 개수와 반복되는 값만으로 표현하는 방법입니다.
WWWWWWWWWWWWBWWWWWWWWWWWWBBBWWWWWWWWWWWWWWWWWWWWWWWWBWWWWWWWWWWWWWW
위와 같은 문자열이 있다고 해봅시다. 위를 런 렝스 부호화를 적용하면 다음과 같이 압축할 수 있습니다.
12WB12W3B24WB14W
’12개의 W, (한 개의) B, 12개의 W, 3개의 B, 24개의 W, (한 개의) B, 14개의 W’로 해석되는 것이죠.
압축 전에는 67글자였지만, 압축 후에는 단지 16글자만으로 표현할 수 있게 되었습니다.
이때 데이터의 크기는 ‘67바이트’에서 ‘16바이트’로 줄었으므로 압축률은 약 4.18이 되는 것이죠!
압축 과정에서 데이터 손실이 없었기 때문에 다시 디코딩해도 원본의 손실없이 데이터를 다시 불러올 수 있습니다.
각 압축 방식에 대해 정답은 없지만 성격에 따라 다음과 같은 점을 고려할 수는 있겠죠.
특정 웹사이트는 손실 압축을 통해 파일 크기를 크게 줄여 저장 공간을 절약함으로써 사이트 성능과 사용자 경험을 향상시킬 수 있는 반면, 고품질 사진이 필요한 웹사이트는 무손실 압축을 사용하는 것이 더 적합할 것 입니다.
초기 압축 알고리즘의 태동
섀넌의 정보 이론

클로드 섀넌은 디지털 시대의 아버지로 불릴 정도로 여러 업적을 세웠는데요, 데이터의 효율적인 전송과 저장에 대한 수학적 모델을 제공하고, 오늘날의 통신 시스템이나 데이터 압축과 같은 기초를 형성했습니다.
당시 전화, 전신 등 통신 시스템이 점점 복잡해지면서 신호의 효율적 전송과 오류 없는 정보 전달이 중요한 과제로 대두되었습니다.
섀넌의 혁신은 “정보”를 의미(meaning)와 분리하여, 오직 ‘신호의 선택 가능성’과 ‘불확실성 감소’라는 관점에서 수학적으로 정의했다는 점입니다.
여기서 정보를 “불확실성을 줄이는 정도”로 보고, 이를 엔트로피(Entropy)라는 개념으로 정량화했습니다.
예를 들어, 동전 던지기(앞/뒤 확률 50%)의 엔트로피는 1bit이며, 이는 정보를 전달하는 데 필요한 최소 비트 수를 의미합니다.
이전에는 의사소통이 단순한 메시지 전달로 여겨졌지만, 섀넌은 정보를 측정, 정량화, 최적화할 수 있다는 개념을 제시한 것이죠.
섀넌-파노 부호화(Shannon-Fano coding)
섀넌과 로버트 파노가 공동 개발한 이 부호화 기술은 정보 이론의 엔트로피 개념을 실용화한 사례입니다.
코드의 알고리즘 원리를 알아보면 다음과 같습니다.
• 섀넌 방식: 각 심볼의 등장 확률에 따라 코드워드의 길이를 미리 정하고, 누적 확률의 이진 표현을 이용해 코드를 할당
• 파노 방식: 심볼을 등장 빈도 순으로 정렬한 뒤, 전체 확률이 비슷하도록 두 집합으로 나누고, 각각 0과 1을 할당하며 재귀적으로 분할. 이 과정을 반복해 각 심볼에 고유한 이진 코드를 부여
이를 정말 쉽게 설명해보자면 “자주 나오는 글자는 짧게, 드물게 나오는 글자는 길게 코딩하는 방법” 이라고 정의할 수 있을 것 같습니다.
한 번 예시를 통해 알아보겠습니다.
정보량 = -log₂(확률)
그렇게 되면 확률에 따른 정보량은 다음과 같습니다.
확률 50% → 1비트 필요
확률 25% → 2비트 필요
확률 12.5% → 3비트 필요
이는 “희귀할수록 더 많은 정보를 담고 있다”는 것을 의미합니다.
여기서 파노의 방법을 예시와 함께 알아보겠습니다.
심볼: A(40%) B(30%) C(20%) D(10%)
1단계: A(40%) vs BCD(60%) → A=0, BCD=1
2단계: B(30%) vs CD(30%) → B=10, CD=11
3단계: C(20%) vs D(10%) → C=110, D=111
위 파노 방식의 설명을 간단하게 정리해봤는데요, 다음과 같이 구분할 수 있을 것 같습니다.
정렬: 확률 높은 순으로 줄세우기
분할: 전체를 반반(비슷하게) 나누기
코딩: 한쪽은 ‘0’, 다른쪽은 ‘1’ 붙이기
반복: 각 그룹을 또 반반 나누기
그렇게 되면 최종 결과는 A=0, B=10, C=110, D=111라는 심볼이 완성되죠.
섀넌-파노 부호화는 효율적인 가변 길이 코드를 생성하지만, 동일 확률 분할 시 발생하는 비최적화 문제로 인해 항상 최적의 코드를 보장하지는 않습니다.
하지만 무손실 압축의 시조로써 현대 정보 이론의 출발점이라는 의의가 있습니다.
허프만 부호화(Huffman Coding)
1952년 미국 MIT 대학의 박사 과정을 밟고 있던 데이비드 허프만은 《A Method for the Construction of Minimum-Redundancy Codes》라는 논문을 발표합니다.
허프만은 문자별 빈도를 고려해 평균 코드 길이를 최소화하는 최적의 부호화 방식을 고안했고, 이는 기존의 고정 길이 부호 방식(예: 아스키 코드)보다 훨씬 효율적이었습니다.
허프만의 알고리즘을 텍스트로 보자면 다음과 같습니다:
- 초기화 : 모든 기호를 출현 빈도수에 따라 나열
- 단 한 가지 기호가 남을 때까지 아래 단계를 반복
3. 목록으로부터 가장 빈도가 낮은 것을 2개 고른다.
4. 그 다음 허프먼이 두가지 기호를 부모 노드를 가지는 부트리를 구성하고 자식노드를 생성한다. 부모 노드 단 기호들의 빈도수를 더하여 주 노드에 할당하고 목록의 순서에 맞도록 목록에 삽입한다.
5. 목록에서 부모노드에 포함된 기호를 제거한다.
설명만으로는 잘 와닿지 않으니 예시를 한 번 살펴보겠습니다.
먼저 다음과 같은 데이터가 주어진다고 가정해봅시다.
빈도 순으로 정렬한 데이터에서 가장 작은 2개 합칩니다. -> A(5) + B(9) = 14
그렇게 되면 현재 목록은 C(12) - D(13) - AB(14) - E(16) - F(45) 이와 같습니다.
이걸 트리로 구성해보겠습니다.
100(루트)
/ \
F(45) 55
/ \
CD(25) ABE(30)
/ \ / \
C(12) D(13) AB(14) E(16)
/ \
A(5) B(9)이제 bit를 할당해보겠습니다.
100(루트)
/ \
0/ \1
F(45) 55
/ \
0/ \1
CD(25) ABE(30)
/ \ / \
0/ \1 0/ \1
C(12) D(13) AB(14) E(16)
/ \
0/ \1
A(5) B(9)자주 나오는 F는 1비트를 드물게 나오는 A,B는 4비트 할당하게 됩니다.
허프만 부호화의 핵심은 문자나 심볼의 등장 빈도에 따라 자주 등장하는 심볼에는 짧은 이진 코드를, 드물게 등장하는 심볼에는 긴 이진 코드를 할당하는 것입니다.
허프만 부호화가 가지는 의의는 엔트로피 부호화(Entropy Encoding)로써, 데이터의 통계적 중복성을 효과적으로 제거하여 평균 부호 길이를 이론적 한계(엔트로피)에 가깝게 줄였다는 점입니다.
상용 압축 기술과 특허 시대
LZW와 GIF의 상업화
1980년대 후반, 컴퓨터 그래픽과 인터넷의 확산과 함께 효율적인 이미지 압축 기술이 필요해졌습니다.
이 시기 개발된 GIF(Graphics Interchange Format)는 LZW(Lempel-Ziv-Welch) 무손실 압축 알고리즘을 채택해 이미지 파일 크기를 크게 줄일 수 있었고, 곧 인터넷과 소프트웨어 산업에서 표준 포맷으로 자리잡았습니다.
당시 LZW 알고리즘은 공개 논문과 기사로 널리 알려져 있었기 때문에, 많은 개발자와 기업들은 이를 자유롭게 사용할 수 있다고 생각했습니다.
Unisys 특허 사건
하지만 LZW 알고리즘은 Unisys과 IBM이 특허를 보유하고 있었고, 1990년대 중반이 되어서야 이 사실이 널리 알려졌습니다.
Unisys와 CompuServe는 GIF 포맷에 대한 라이선스 계약을 체결하고, 상업적 소프트웨어와 웹 서비스에 LZW 사용료를 부과하기 시작했습니다.

이로 인해 개발자들 및 커뮤니티에서는 강한 반발이 일어났고, “Burn All GIFs Day”와 같은 캠페인이 등장했습니다.
특허 논란은 GIF와 LZW의 자유로운 사용을 막았고, 특허 만료(2003~2004년) 전까지 특허료 부담이 지속되었습니다.
이 사건은 소프트웨어 특허의 복잡성과, 공개 표준에 대한 특허 적용이 산업과 인터넷 생태계에 미치는 영향을 대표적으로 보여주는 사례가 되었습니다.
Deflate의 탄생

이러한 특허 논란과 상업적 제약에 대응하기 위해, 1993년 필 캐츠(Phil Katz)는 특허에 구애받지 않는 새로운 압축 알고리즘인 Deflate를 개발했습니다.
Deflate는 LZ77과 허프만 코딩을 결합해 높은 압축률과 빠른 속도를 제공하면서도, 특허 문제 없이 누구나 자유롭게 사용할 수 있도록 설계되었습니다.
무엇보다 웹의 시대가 도래하면서 전송 속도와 대역폭 용량 개선을 위해 HTTP 압축이라는 기술의 필요성이 생겼는데 이 알고리즘 방식이 채택되기도 했죠.
ZIP, Gzip, PNG 등 다양한 파일 포맷과 인터넷 표준에서 널리 채택되었고, 특허 이슈로부터 자유로운 오픈 포맷의 대표적 성공 사례가 되었습니다.
Gzip

gzip은 ZIP과 같이 DEFLATE 알고리즘을 따르지만, 여러 파일을 하나의 파일로 압축하는 옵션이 없다는 점에서 차이가 납니다.
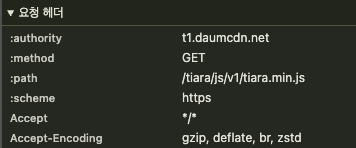
웹 서버로 리소스를 요청할 때 Request Header의 accept-encoding을 볼 수 있습니다.
브라우저에서 호환되는 압축 정보를 실어 함께 요청하면, 해당하는 압축 방식을 지원하는지 확인하고, 지원한다면 리소스를 압축하여 리소스를 전달하게 됩니다.
Gzip 방식으로 HTTP 리소스를 압축하여 기본 용량보다 70~80% 리소스 사이즈를 줄일 수 있게 되었습니다.
이후에는 구글의 Brotli와 Facebook의 Zstandard도 이어서 등장하면서, Gzip보다 더 높은 압축률과 빠른 속도를 제공하며, 현대 웹과 시스템 환경에서 점점 더 많이 사용되고 있습니다.
이들은 효율적인 데이터 전송을 위한 차세대 압축 알고리즘으로 자리 잡아가고 있습니다.
맺음
앞으로 미래 압축기술은 어떨까요?
최근에는 AI, 특히 딥러닝을 활용한 압축 기술이 주목받고 있는데요, 기존 압축 알고리즘은 주로 데이터 내 반복 패턴이나 통계적 특성을 분석해 효율적으로 인코딩했지만, AI 기반 압축은 대규모 데이터셋에서 패턴을 직접 학습하여 더 높은 압축률과 품질을 달성하고 있다고 합니다.
샤논 한계에 따르면 데이터를 아무리 효율적으로 압축해도 그 데이터가 가진 엔트로피(불확실성, 정보량) 이하로는 압축할 수 없다는 한계가 있는데, 양자 컴퓨터의 발전이 이를 해결해줄수도 있지 않을지 생각해봅니다. (전문가가 아니라 하하..)
역사를 다루는 글은 언제나 재밌네요. 이번에도 읽어주셔서 감사합니다.